对于断言 ASSERT 的理解
昨天看了《代码大全》的“防御式编程”章节,解惑了长期以来自己对于断言的理解。
书中给了使用断言的指导意见,如下
- 用错误处理代码来处理预期会发生的状况,用断言来处理绝不应该发生的状况。
- 避免把需要执行的代码放到断言中
- 用断言来注解并验证前条件和后条件
-
对于高健壮性的代码,应该先使用断言再处理错误
对来源于内部系统的可靠的数据使用断言,而不要对外部不可靠的数据使用断言,对于外部不可靠数据,应该使用错误处理代码。断言可以看成可执行的注释。
#ifndef _ASSERT_EX_H
#define _ASSERT_EX_H
#include <stdlib.h>
#include <stdio.h>
#ifdef _DEBUG
#define _ASSERT(exp, message) { \
if (!(exp)) { \
fprintf(stdout, "Assertion failed: \"%s\"\nMessage: \"%s\"\nline: %d\nfile: \"%s\"\n", \
#exp, message, __LINE__, __FILE__); \
exit(EXIT_FAILURE); \
} \
}
#else
#define _ASSERT(exp, message)
#endif
#endif //_ASSERT_EX_H
参心大地坐标与参心空间直角坐标的转换
参心大地坐标转换为参心空间直角坐标
$$\begin{cases} & X=(N+H)\cos{B}\cos{L} \\ & Y=(N+H)\cos{B}\sin{L} \\ & Z=[ N(1- \mathit{e}^2)+H) ]\sin{B} \end{cases}$$公式中,$N$ 为椭球面卯酉圈的曲率半径,$\mathit{e}$ 为椭球的第一偏心率:$$\mathit{e}^2 = \frac{a^2-b^2}{a^2}$$ $a$ ,$b$ 椭球的长短半径 $$N=\frac{a}{\sqrt{1-\mathit{e}^2\sin^2B}}$$
参心空间直角坐标转换为参心大地坐标
$$\begin{cases} & L=\arctan\left(\frac{Y}{X}\right) \\ & B=\arctan\left(\frac{Z\left(N+H\right)}{\sqrt{\left(X^2+Y^2 \right)\left[N\left(1-\mathit{e}^2 \right) + H \right]}}\right) \\ & H=\frac{Z}{\sin B}-N\left(1-\mathit{e}^2 \right) = \frac{\sqrt{X^2 + Y^2}}{\cos B} - N \end{cases} $$
大地经度 $L$ ,$B$ 求解要考虑 $Y$ 和 $Z$ 的正负。
大地纬度 $B$ 的计算比较复杂,变换后 $$\tan B = \frac{Z+N\mathit{e}^2\sin B}{\sqrt{X^2 + Y^2}}$$ 上式中右端有待定量 $B$ ,需要迭代计算。迭代时可取 $$\tan B_1=\frac{Z}{\sqrt{X^2+Y^2}}$$ 用 $B$ 的初值 $B_1$ 计算 $N_1$ 和 $\sin B_1$ ,然后继续迭代,直至最后两次 $B$ 值之差小于允许误差为止。
由于左、右两端具有不同的三角函数,这对于迭代很不方便。为克服这一缺点,建议采用下面的迭代公式:
$$N=\frac{c}{V}=\frac{c}{\sqrt{1+{e'}^2\cos^2 B}}$$
$$\frac{1}{\cos^2 B}=1+\tan^2 B$$
整理得 $$\tan B = \frac{Z}{\sqrt{X^2+Y^2}}+\frac{ce^2\tan B}{\sqrt{X^2+Y^2} \cdot \sqrt{1+{e'}^2+\tan^2 B}}$$ 因此,$$t_{i+1}=t_0+\frac{pt_i}{\sqrt{k+t_i^2}}$$ 式中 $$\begin{cases} & t_0=\frac{Z}{\sqrt{X^2+Y^2}} \\ & p=\frac{ce^2}{\sqrt{X^2+Y^2}} \\ & k=1+{e'}^2 \\ & c=a\sqrt{1+{e'}^2} \\ & {e'}^2 = \frac{a^2-b^2}{b^2} \end{cases}$$ $t_i$ 为前一次迭代值,第一次迭代令 $t_i=t_0$ 。
参考资料:
《大地测量基准与坐标转换》,姚宜斌,武汉大学测绘学院卫星应用工程研究所,2006.03. PDF链接
《大地测量学基础》,孔祥元 郭际明 刘宗泉,武汉大学出版社, P103.
四参数转换使用的公式
设四参数转换 尺度 为 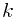 ,旋转角为
,旋转角为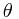 ,坐标系位移量分别为
,坐标系位移量分别为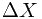 ,
,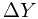 则单点转换公式为
则单点转换公式为
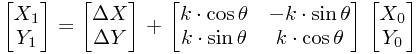
变换后的矩阵形式为
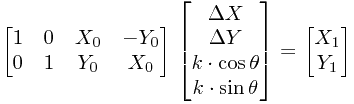
这就是类似 ![\[BX=A\] \[BX=A\]](/user_files/tisyang/epics/c402e18291c5d7abd5daa0ed5044aed18f405dfe.png) 的平差式
的平差式
所以可知
![\[X=\bigl(B^TB\bigr)^{-1}B^TA\] \[X=\bigl(B^TB\bigr)^{-1}B^TA\]](/user_files/tisyang/epics/f180f7812d1d0629894a5c09da76fd27a3c0e883.png)
PS:实验下学  怎么写公式
怎么写公式
DLL 导出函数以及DEF文件的作用相关链接
一下午都在研究 def 文件为什么能无修饰名的导出函数名到dll,然后找了好几篇文章,推荐两个:
http://archive.cnblogs.com/a/2196642/ 编写DLL所学所思(1)——导出函数
http://hi.baidu.com/luosiyong/blog/item/3d68f3fc68a01098b801a045.html dll的def文件与__declspec(dllexport)导出函数方式比较
def 文件不会影响生成的导入库文件(.lib),def文件可以指定导出别名。在 C 和 C++ 混合DLL编程中就需要注意了,def 文件并不能很自然地 隐式链接调用DLL,因为头文件声明的函数名和导入库(.lib)中的符号名并不对应(除非使用 extern "C" 声明),因为 C 编译器和 C++编译器(或者不同C++编译器)中的函数名修饰规则并不相同。
Ruby 的小角度7参数转换简单描述
小角度7参数转换的 Ruby 使用 Matrix的简单描述
小角度的7参数坐标系转换可以化简原本的转换参数公式,最后如下图片描述
这是一段根据3个点对的坐标来求解转换额外一点的对应坐标的 Ruby代码,使用了Ruby标准库里的 Matrix,很方便的:
require 'matrix'
def buildBUnit(*p)
a = []
a[0, 7] = 1, 0, 0, p[0], 0, -p[2], p[1]
a[7, 7] = 0, 1, 0, p[1], p[2], 0, -p[0]
a[14, 7] = 0, 0, 1, p[2], -p[1], p[0], 0
a
end
def cutDown(*p, count)
a = []
row = 0
while row < (p.count.to_f / count).ceil
a << p[row * count, count]
row += 1
end
a
end
def buildB(*p)
a = []
p.each {|point| a += buildBUnit(*point) }
Matrix[*(cutDown(*a, 7))]
end
def buildA(*p)
Matrix.column_vector(p.flatten)
end
m = [[ 30.55876333, 117.2395818, 13.09], [30.55882632, 117.23958408, 13.188], [ 30.55876333, 117.23968333, 13.09]]
p = [[13.127, -3.579, 10.143], [13.090, 3.434, 10.200], [3.127, -3.579, 10.143]]
B = buildB(*p)
A = buildA(*m)
BT = B.transpose
temp = BT * B
X = temp.inv * BT * A
bas = [47.850, -0.020, 3.399]
trans = Matrix[*cutDown(*buildBUnit(*bas), 7)]
MM = trans * X
p MM
#够简单的。。。。

